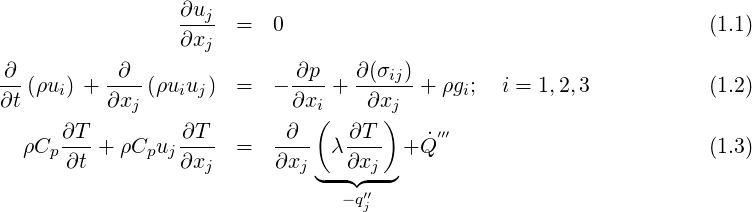
Considering the motion of a Newtonian fluid with constant properties (density and viscosity) velocity
There is a need for closure laws for the viscous stress tensor
Fourier law is also used, which assumes that the thermal conductivity
In some cases, solids or fluids do not have isotropic properties for heat conduction. In this case,
thermal conductivity
where
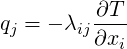 | (1.6) |
takes into account the anisotropy of heat conduction.
The evolution equation for the scalar
where
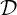
We start with the discretised version of the momentum equations given by,
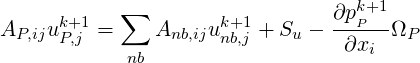 | (1.8) |
where
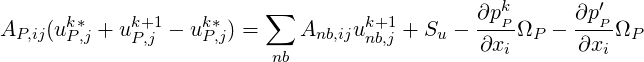 | (1.9) |
Applying operator splitting we obtain two equations,
If the first term in the RHS is approximated as,
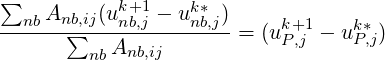 | (1.12) |
based on the idea that the cell–centre velocity correction is a coefficient weighted average of the velocity
corrections at the neighbouring cells, we obtain the
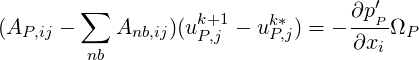 | (1.13) |
Denoting
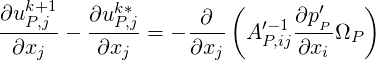 | (1.14) |
For incompressible single–phase flows, two–phase flows using interface tracking, or for homogeneous flow
models, we set the expectation on the divergence of
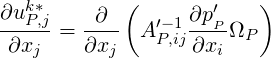 | (1.15) |
The integral form of Eq. (1.15) is solved. Integrating using the divergence theorem we get the following discretised equation,
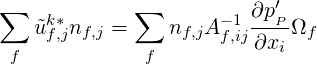 | (1.16) |
where, the velocity at the faces
For axisymmetric geometries, the continuity equation is given by
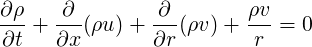 | (1.17) |
or
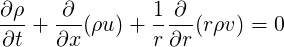 | (1.18) |
where
The axial and radial momentum conservation equations are given by
![[ ( )]
∂-(ρu) + ∂--(ρuu )+ 1-∂-(rρvu ) = - ∂p-+-∂- μ 2∂u-- 2-(∇ ⋅⃗v)
∂t ∂x r ∂r ∂x ∂x ∂x 3
1 ∂ [ ( ∂u ∂v )]
+ r∂r- rμ ∂r-+ ∂x- + (1.19)
(1.20)](TransAT_algorithms_handbook16x.png)
![∂ ∂ 1 ∂ ∂p ∂ [ ( ∂v ∂u )]
--(ρv) + ---(ρuv )+ ----(rρvv) = - ---+ --- μ ---+ ---
∂t ∂x [ r(∂r ∂r)] ∂x ∂x ∂r
+ 1-∂--rμ 2∂v-- 2-(∇ ⋅⃗v) - 2μ-v + 2-μ-(∇ ⋅⃗v) (1.21)
r ∂r ∂r 3 r2 3 r](TransAT_algorithms_handbook17x.png)
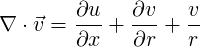 | (1.22) |
or
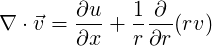 | (1.23) |
This section describes the compressible flow modelling capabilities of TransAT.
Equations that are solved for compressible flows are the following (Poinsot & Veynante, 2001):
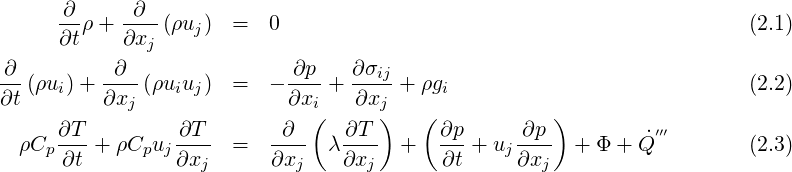
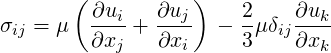 | (2.4) |
and Φ is the viscous dissipation of kinetic energy. Thermodynamical properties
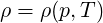 | (2.5) |
Equations that are solved for compressible n-phase flows are given belows. In the current version, compressible flow is only available for the homogeneous model (no drift velocity), without phase change.
with the subscript
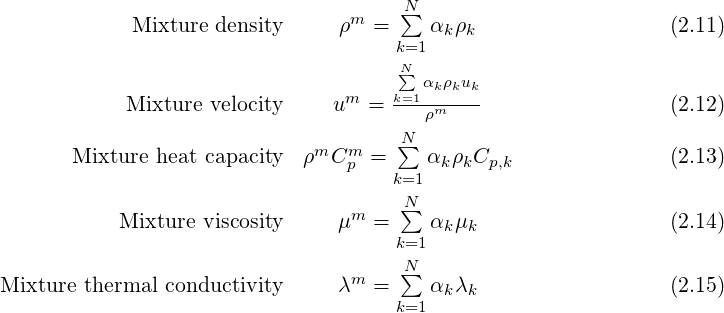
The equations used to model compressible flows with Level-Set method are the following. In the current version, phase change is not available for compressible flows.
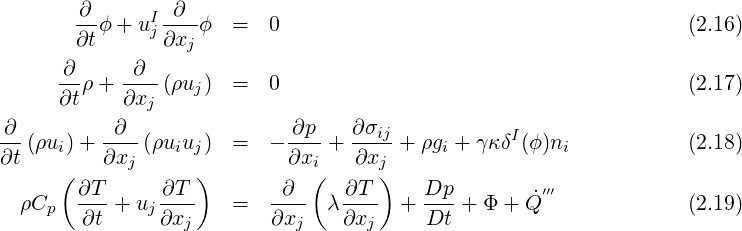
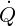 is the volumetric heat source. Material
properties are updated using
is the volumetric heat source. Material
properties are updated using
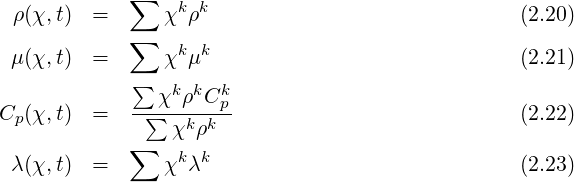
The simplest way to link density, pressure and temperature is to use the ideal gas equation of state. This is applicable only for gases. It reads
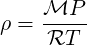 | (2.24) |
where 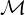
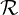
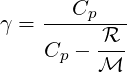 | (2.25) |
where 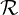
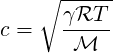 | (2.26) |
The Stiffened Gas Equation is an equation of state used for water under very high pressures. This equation can be applied for certain other liquids, but specific heat capacity is likely to be miscalculated. It reads
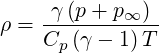 | (2.27) |
The fluid will behave as an ideal gas at pressure
The different parameters must respect the equality
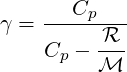 | (2.28) |
where 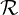
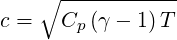 | (2.29) |
The Tait equation is an equation of state derived for water and sea-water Cooke & Chen (1992). Density of water as a function of pressure can then be expressed as
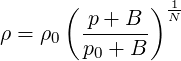 | (2.30) |
where
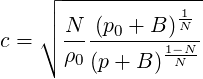 | (2.31) |
The Tait equation of state is also available in
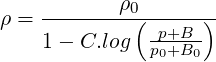 | (2.32) |
where: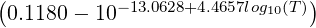 ,
,
Another possibility when working with water is to use the Peng-Robinson equation of state.
In general the Peng-Robinson equation of state writes:
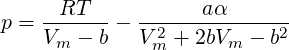 | (2.33) |
Started from this equation a cubic equation for the molar specific volume is obtained and solved. The density is then obtained using following relation:
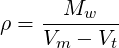 | (2.34) |
with
The Peng-Robinson equation of state is also available for water vapour. The implementation is similar to the liquid state implementation.
The viscosity
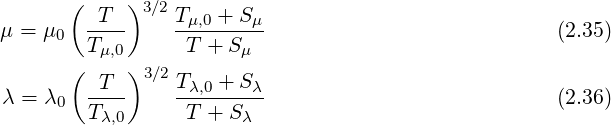
The phasic continuity equation is written below in the volume fraction and mass fraction forms as,
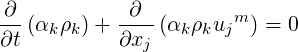 | (2.37) |
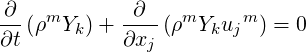 | (2.38) |
where superscript
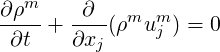 | (2.39) |
Equation (2.38) can also be written in a material derivative form as follows, which will be useful in the derivation of the pressure equation,
![[ ] [ m m m]
ρm ∂Yk- + um ∂Yk- + Y ∂ρ--+ ∂ρ-u--- = 0
∂t j ∂xj k ∂t ∂xj](TransAT_algorithms_handbook44x.png) | (2.40) |
and plugging Eq. 2.39 gives
![[ ]
m ∂Yk- m ∂Yk-
ρ ∂t + uj ∂xj = 0](TransAT_algorithms_handbook45x.png) | (2.41) |
We introduce now the notation of material derivative advected by the mixture velocity as,
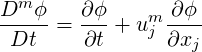 | (2.42) |
where
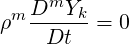 | (2.43) |
An equation for the evolution of the pressure of a multiphase system is derived here. It is based on a
single pressure, single temperature assumption where the pressure
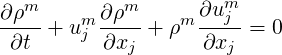 | (2.44) |
This can be rewritten in the material derivative notation as,
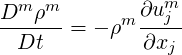 | (2.45) |
Taking
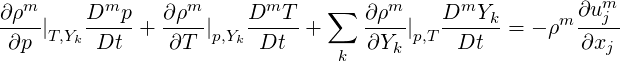 | (2.46) |
To evaluate the constrained derivatives, we start with the definition of density with respect to phasic densities and mass fractions.
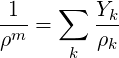 | (2.47) |
where
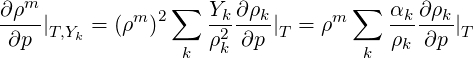 | (2.48) |
Similarly the derivative at constant (
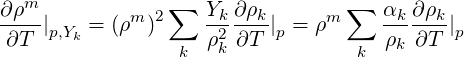 | (2.49) |
The derivative of density with respect to
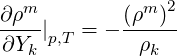 | (2.50) |
Additionally we write the mixture temperature equation 2.9 using material derivatives
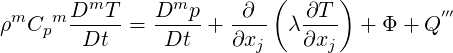 | (2.51) |
where Φ is the viscous dissipation of kinetic energy. The material derivative of
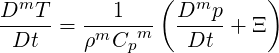 | (2.52) |
where Ξ represents the entropic part of heat transfer (the last three terms in the RHS of Eq. (2.51)).
Plugging Eqs. (2.48)-(2.50), Eq. (2.52) and Eq. (2.43) into Eq. (2.46), we obtain
![[ ( ) ] [ ] m
∑ m αk- ∂ρk- ---1---∂ρk- Dmp-- ∑ m αk-∂ρk- ---Ξ--- m∂u-j
ρ ρk ∂p |T + ρmCpm ∂T |p Dt + ρ ρk ∂T |p ρmCpm = - ρ ∂xj
k k](TransAT_algorithms_handbook57x.png) | (2.53) |
where the identity
In the limit of incompressible flow, the LHS of Eq. (2.53) can be set to zero, giving,
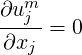 | (2.54) |
For the limit of compressible single-phase flow, we set
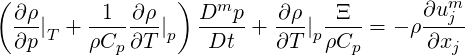 | (2.55) |
Note that for an ideal gas
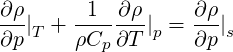 | (2.56) |
where
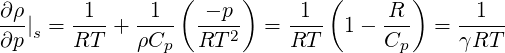 | (2.57) |
where we have used the relationships
A conservative formulation is used for the pressure solver in the case of reactive, compressible flows. We
start with Eq. (1.13) and multiply it through by
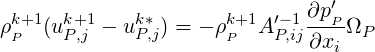 | (2.58) |
Taking the divergence of the above equation we obtain:
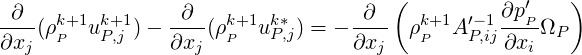 | (2.59) |
Splitting
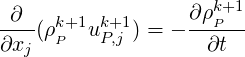 | (2.60) |
we obtain,
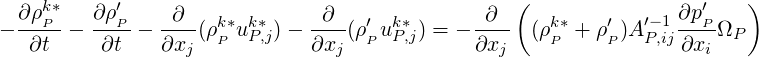 | (2.61) |
Neglecting the
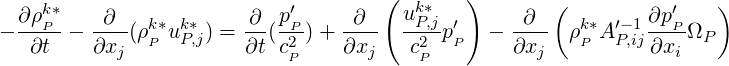 | (2.62) |
The solver for compressible flows is based on the work of Karki & Patankar (1989) andMichelassi
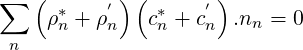 | (2.63) |
where
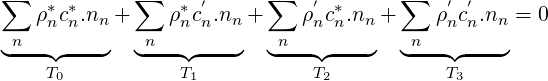 | (2.64) |
Where
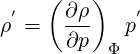 | (2.65) |
where Φ is the temperature or entropy, whether we use the hypothesis of isothermal or entropic
transformation.
Equation 3.13 is then rewritten for compressible flows
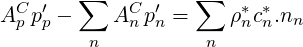 | (2.66) |
where

In this section, we note
For high velocities, an upwind scheme can be used. We can thus write

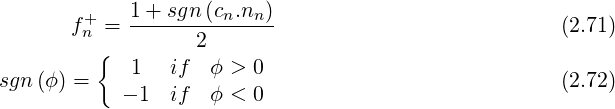
![[(∂ ρ) ]
Acowrr = max (cw.nw,0) --- (2.73)
[(∂p ) Φ]W
corr ∂ρ-
A e = - min (ce.ne,0) ∂p (2.74)
Φ(E )
C ∑ corr [( ∂ρ) ] ∑ ∑
SP = A n + --- ( min (cn.nn,0) - max (cn.nn,0))(2.75)
n ∂p Φ P n=W,S,B n=E,N,T](TransAT_algorithms_handbook74x.png)
This scheme can be used for compressible flows at low velocities. We have

![( [( ∂ρ ) ] [( ∂ρ) ] )
Acowrr = fw (cw.nw,) fw --- + (1- fw ) --- (2.78)
(∂p[ Φ( W) ] ∂p[( Φ P) ] )
corr ∂ρ- ∂ρ-
A e = - (1- fe)(ce.ne, ) fe ∂p Φ P + (1 - fe) ∂p Φ E (2.79)
∑ ( [( ) ] [( ) ] )
SCP = Acnorr + (1- fw )(cw.nw, ) fw ∂ρ- + (1- fw ) ∂ρ- (2.80)
n ∂p Φ W ∂p Φ P
( [( ∂ρ) ] [(∂ ρ) ] )
- (fe)(ce.ne,) fe --- + (1- fe) --- (2.81)
∂p Φ P ∂p Φ E](TransAT_algorithms_handbook76x.png)
When performing an unsteady simulation, an extra-term must be added to the compressible
contribution
![[( ) ]
SCP,unsteady = SCP,steady - -Ω- ∂ρ-
Δt ∂p Φ P](TransAT_algorithms_handbook77x.png) | (2.82) |
where Ω is the cell volume and Δ
The partial differential equations governing steady incompressible flows in nonorthogonal coordinates may be written in the following general form (Patankar, 1980):
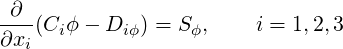 | (3.1) |
where the coefficients
Eq. 3.1 has two important features which are worthy of mention: (i) it is in conservation form which implies all terms arising from the divergence operator are under differential operators, and (ii) it does not contain second-derivatives of coordinates (curvature terms) which are very sensitive to grid smoothness.
Integrating Eq. 3.1 over a typical control volume centered at P (Figure 3.1) leads to a flux balance equation
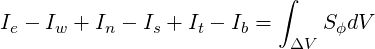 | (3.2) |
where
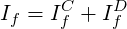 | (3.3) |
Eq. 3.2 involves no approximation and represents a finite-volume analogue of the differential equation ( 3.1).
The convective contribution in Eq. 3.3 can be written as:
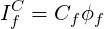 | (3.4) |
where
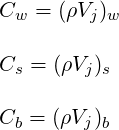 | (3.5) |
The determination of
The
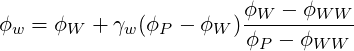 | (3.6) |
where
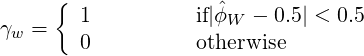 | (3.7) |
All the schemes but Hybrid are implemented in the program in a deferred way proposed by Khosla & Rubin (1974)
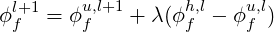 | (3.8) |
where
All the schemes but Hybrid require two upstream nodes for each cell-face, which will involve a value outside the solution domain for a near-boundary control volume. Therefore in the program the Hybrid scheme is used for all the control volumes adjacent to boundaries.
The diffusive flux
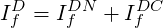 | (3.9) |
The first part
![IDwN = Dw (ϕP - ϕW );withDw = [Γ ϕ∕ΔV ]w](TransAT_algorithms_handbook87x.png) | (3.10) |
The second part
The source terms
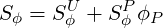 | (3.11) |
The coefficient
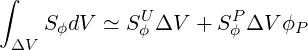 | (3.12) |
After replacing all the terms in Eq. 3.2 by their discretised analogies, the following difference equation results in:
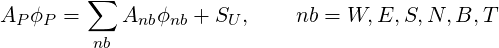 | (3.13) |
where
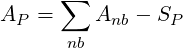 | (3.14) |
The main coefficients
In order to stabilise the iterative solution process, it is often necessary to under-relax the current solution by
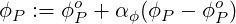 | (3.15) |
where
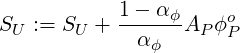 | (3.16) |
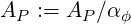 | (3.17) |
The most frequently encountered boundary conditions, i.e., inflow, outflow, symmetry and rigid wall conditions, are implemented in the program. The pressures at all the boundary nodes are evaluated by linear extrapolation from values at interior nodes. The program also provides a provision allowing the user to specify boundary conditions other than these four types.
At the inflow planes, the value of each variable
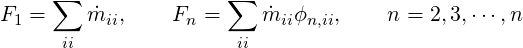 | (3.18) |
with
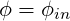 | (3.19) |
where the summation index ii runs over all the inlet computational nodes, ṁ is the mass flux and the
subscript ”in” refers to the inlet values.
At the outflow planes, the stream-wise gradients of all variables are set to zero, implying a fully
developed flow condition. In addition, the velocities
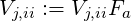 | (3.20) |
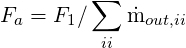 | (3.21) |
where ii runs over all the outlet computational nodes and ṁ
For pressure outflows with a pressure loss coefficient
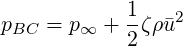 | (3.22) |
where
At the symmetry planes, the normal velocity component and the normal gradients of other variables are
set to zero. The convective and normal diffusive fluxes
At the rigid walls, the no-slip condition is used for laminar flows, i.e., the velocity components of the
flow are set to those of the wall. The standard wall-function approach (Launder & Spalding, 1974) is
used for turbulent flows. In this, the resultant wall shear stress 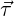
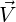 by
by
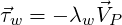 | (3.23) |
where
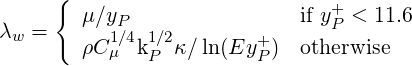 | (3.24) |
 | (3.25) |
the subscript
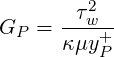 | (3.26) |
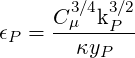 | (3.27) |
For inflow conditions one can define the total pressure
For an ideal gas, isentropic expansion (
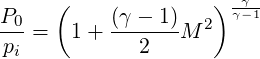 | (3.28) |
Velocity can then be obtained by substituting
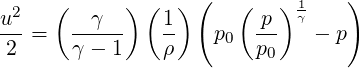 | (3.29) |
For a liquid phase, either with compressible and incompressible formulation, the density is a very weak
function of pressure, or in other words, density remains almost constant even for large variations in
pressure. The relationship between
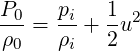 | (3.30) |
The
The general form of the Bernoulli equation can be derived as follows from the conservation of mass and conservation of total energy equations for steady one-dimensional compressible flow where entropy producing terms such as heat conduction, heat sources, viscous dissipation etc. have been set to zero.
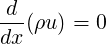 | (3.31) |
and
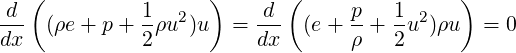 | (3.32) |
Using the product rule and using the conservation of mass equation, we obtain,
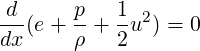 | (3.33) |
Since we are interested in the process from state 1 to 2 we can write the above equation as,
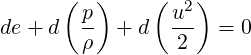 | (3.34) |
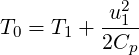 | (3.36) |

T0 T0 T1](TransAT_algorithms_handbook116x.png) | (3.37) |
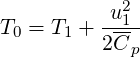 | (3.38) |
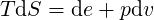 | (3.39) |
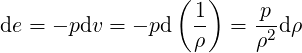 | (3.40) |
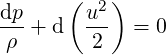 | (3.41) |
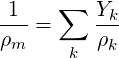 | (3.42) |
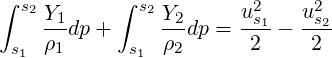 | (3.43) |
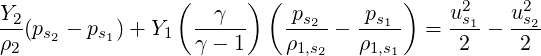 | (3.44) |
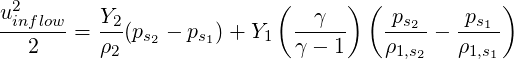 | (3.45) |
To find the pressure coefficient arising out of specifying the inflow velocity using the isentropic relation for the ideal gas, we take the derivative of Eq. (3.29) with respect to pressure to obtain,
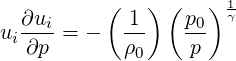 | (3.46) |
Multiplying both sides by the square of the inflow cell area
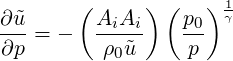 | (3.47) |
or rewriting in terms of
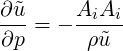 | (3.48) |
The residuals are defined for the continuity equation as:
![[ ]
∑ 1∕2
RL2 = (Ce - Cw + Cn - Cs + Ct - Cb)2ii ∕F1
ii](TransAT_algorithms_handbook128x.png) | (3.49) |
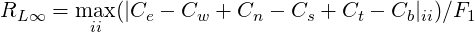 | (3.50) |
For all the other equations the residuals are defined as:
![[ ]1∕2
∑ ∑ 2
Rm (L2 ) = ( Anbϕnb + SU - AP ϕP)ii ∕Fm (nb = E, W,N, S,T, B)
ii nb](TransAT_algorithms_handbook130x.png) | (3.51) |
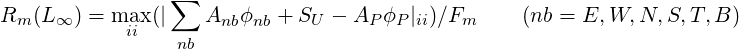 | (3.52) |
where ii runs over all the computational nodes and
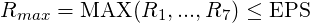 | (3.53) |
where EPS is the convergence criterion prescribed by the user.
The sequence in which the calculation is carried out is as follows:
Sequence of steps b to f is repeated until the convergence criterion (Eq. 3.53) is satisfied.
A complete sequence of steps b to f is defined as an
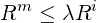 | (3.54) |
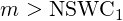 | (3.55) |
where
The species equation for every species k can be written as (Poinsot & Veynante, 2001)
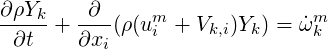 | (4.1) |
Where 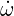
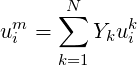 | (4.2) |
where
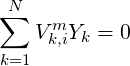 | (4.3) |
The diffusion velocities are determined by the multicomponent diffusion equation which can be derived for a low density ideal gas (Williams, 1958; R.J. Kee, 2003):
![N∑ XkXj ∇p
∇Xk = ------(vj - vk + (Yk - Xk)--
j=1 Dkj p
ρ ∑N N∑ XkXj DT,j DT,k ∇T
+-- YkYj(fk - fj) + [-----(------ -----)]----
pj=1 j=1 ρDkj Yj Yk T](TransAT_algorithms_handbook139x.png) | (4.4) |
where
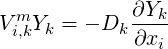 | (4.5) |
The species equation is then:
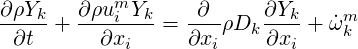 | (4.6) |
The species equation in terms of mole fractions reads:
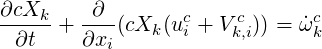 | (4.7) |
Where c is the total concentration, 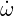
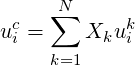 | (4.8) |
For the diffusion velocities the resulting constraint is:
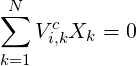 | (4.9) |
In general
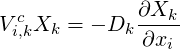 | (4.10) |
This finally results in:
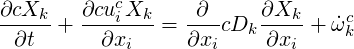 | (4.11) |
As this equation was derived under the assumption of ideal gas, constant temperature and constant pressure, it can only be applied in the case of constant concentration.
One can write the transport equation directly for concentration of species k (
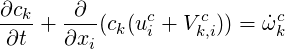 | (4.12) |
The concentration weighted velocity is then
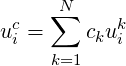 | (4.13) |
with the constraint:
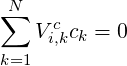 | (4.14) |
The diffusion velocity is then written according to Ficks law as:
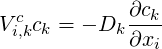 | (4.15) |
Which results in the concentration equation:
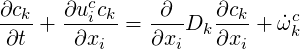 | (4.16) |
For constant concentration, Eq.(4.16) and Eq.(4.11) are the same but the latter can be used to derive an transport equation for a passive scalar.
In a passive scalar formulation the flow velocity is not determined by mass or concentration averaged
velocities. The velocity field
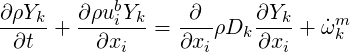 | (4.17) |
One component can be constrained to ensure mass conservation.
As mentioned above the mole fraction formulation of the species equation can not be used for a general
passive scalar as the total concentration can vary in space and time. However by replacing the
concentration averaged velocity by the base velocity
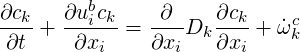 | (4.18) |
In order to apply the mixture fraction approach the passive scalar must obey an equation of the form (Fox, 2003)
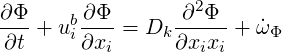 | (4.19) |
Assuming constant D and using the continuity equation this can be rewritten in a form suitable for TransAT
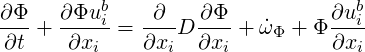 | (4.20) |
This equation is solved for the mixture fraction and progress variable where in the case of the mixture fraction the source term will vanish.
In a laminar flow the chemical source term is determined by Arrhenius rate constants:
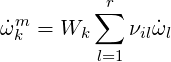 | (4.21) |
where 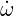
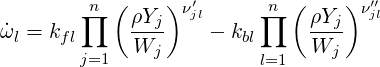 | (4.22) |
and 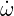
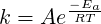 | (4.23) |
where
Besides the specific derivation for a combustion system, mixture fraction and progress variable for a system can be derived in a general way. One tries to make a coordinate transformation from the physical space (in terms of concentration or mass fractions) to a space where as few transported scalars as possible have a chemical source term. Consider a system with three species: reactant A, reactant B, and the product P which take part in the reaction:
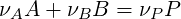 | (4.24) |
All three species fulfill a transport equation of the form
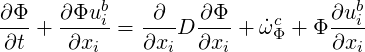 | (4.25) |
where Φ can be replaced by the concentration of the species (
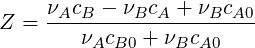 | (4.26) |
To obtain a transport equation for the mixture fraction, Φ in Eq.(4.25) can be replaced by Z where
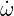
As there is only one reaction in this system the source term of all species is directly linked to the
reaction rate of this reaction. R is defined as the molar reaction rate [mol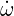
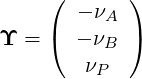 | (4.27) |
The progress variable (
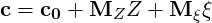 | (4.28) |
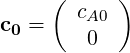 | (4.29) |
and
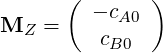 | (4.30) |
If we write the the transport equation (4.25) for
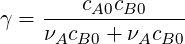 | (4.31) |
This finally yields the concentration of all three species expressed with mixture fraction and progress variable:
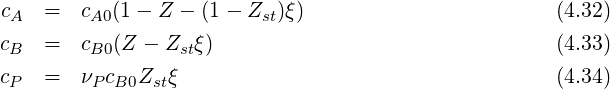
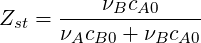 | (4.35) |
The source term for the progress variable in Arrhenius formulation is then
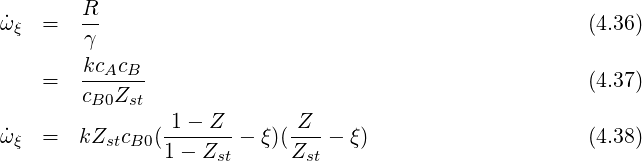
If we define the mixture fraction for mass fractions the mixture fraction definition is slightly different
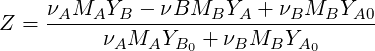 | (4.39) |
As the mixture definition is now in terms of masses the mass stoichiometric coefficients
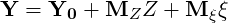 | (4.40) |
From the pure mixing solution we can obtain:
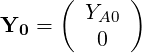 | (4.41) |
and
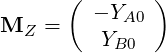 | (4.42) |
Using the same definition as above reaction vector is then
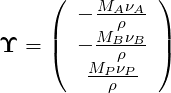 | (4.43) |
As the product mass fraction has already the desired scaling (0
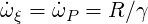 | (4.44) |
Therefore
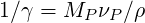 | (4.45) |
and
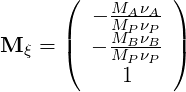 | (4.46) |
From this we get:
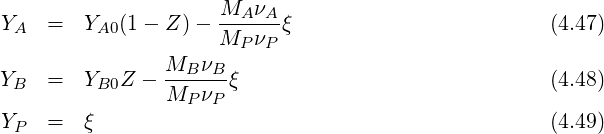
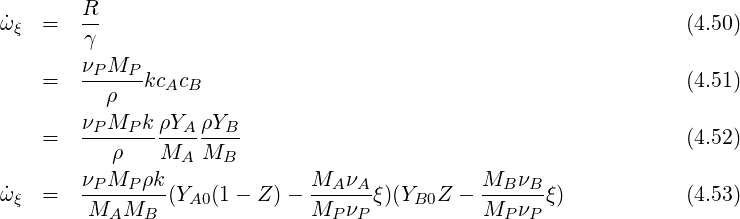

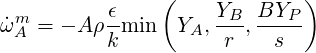 | (4.56) |
From this we conclude that
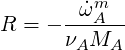 | (4.57) |
Therefore the source term for the progress variable is:
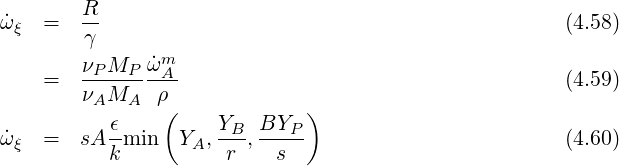
A balance equation can be also written for the temperature
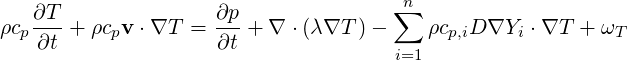 | (4.61) |
where
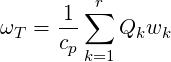 | (4.62) |
where
The vector (
If different diffusivity must considered, the convection velocity of the species must be corrected by
adding a correction velocity 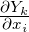 to ensure global mass conservation.
to ensure global mass conservation.
When the species have different densities, the usual Reynolds average gives new unclosed terms
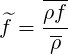 | (4.63) |
where 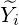 and a fluctuation
and a fluctuation
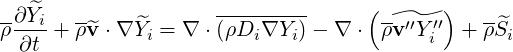 | (4.64) |
In this equation the r.h.s. terms must be modelled.
The species turbulent fluxes 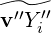 are generally closed using a classical gradient assumption
are generally closed using a classical gradient assumption
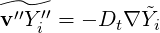 | (4.65) |
where 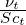 where
where
The laminar diffusive fluxes are generally neglected or retained by adding a laminar diffusivity to the turbulent viscosity in Eq.(4.65).
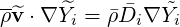 | (4.66) |
where is a “mean” species molecular diffusion coefficient.
The same equation obtained for RANS approach can be obtained with LES, substituting the filter operation to the Favre average and the same terms needs a closure that is achieved using the sub-grid scale viscosity and additional sub-grid scale model for source terms.
In combustion this case is also called
In non-premixed flows the reactions are strictly connected with the mixing and by comparing these two phenomena we can distinguish different reaction regimes. With reference to Figure 4.1, we define “slow” chemistry for the reactions with time scales larger than the micromixing time scale, “fast” chemistry when the chemical time scales are all smaller than the Kolmogorov time scale and “finite-rate” chemistry in the middle. In the following we will consider first the two limiting cases, “frozen” (very-slow) chemistry and “infinitely-fast” chemistry.

For
The importance of the mixture fraction is that it is a conserved quantity, a scalar quantity that is
neither created nor destroyed so the equations for
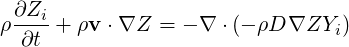 | (4.67) |
Many computational models for combustion are developed with a single mixture fraction which can be used only for two-feed systems. If more than two feeds enter into a combustion chamber, the concept of single mixture fraction can no longer be used. In fact, even if it can formally be extended to multiple mixture fraction variables, it becomes less attractive for modelling because the resulting flamelet equations are defined in a multi-dimensional space.
The usual definition of mixture fraction for non-premixed combustion is best derived for an
homogeneous system in the absence of diffusion. In this case the reaction equation for complete
combustion of hydrocarbon fuel
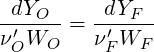 | (4.68) |
where
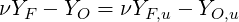 | (4.69) |
where  is the stoichiometric oxygen-to-fuel mass ratio and the subscript
is the stoichiometric oxygen-to-fuel mass ratio and the subscript
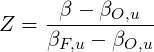 | (4.70) |
where
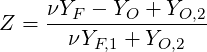 | (4.71) |
where subscript 1 denotes the the fuel stream and 2 the oxidiser stream.
The stoichiometric mixture fraction
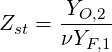 | (4.72) |
The mixture fraction can be related to the commonly used equivalence ratio
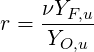 | (4.73) |
The mixture fraction can be also expressed starting from a quantity related to chemical elements. In fact, while the mass of chemical species may change due to chemical reactions, the mass of elements is conserved. (Poinsot & Veynante, 2001; Peters, 2000).
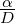 where
where 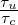 is the ratio between the integral time scale and the chemical
time scale
is the ratio between the integral time scale and the chemical
time scale
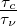 is the ratio between chemical time scale and the Kolmogorov
time. From this it follows that
is the ratio between chemical time scale and the Kolmogorov
time. From this it follows that In our discussion, the most important closure will be the source term 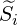 . The simpler model is to neglect
the fluctuations and write the Arrhenius equation with the mean quantity
. The simpler model is to neglect
the fluctuations and write the Arrhenius equation with the mean quantity 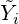 . This approximation is
called the “Arrhenius approach” and the closure relation is simply
. This approximation is
called the “Arrhenius approach” and the closure relation is simply
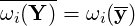 | (4.74) |
This model is relevant only for laminar flow or when chemical time scale are larger than turbulent time
scale (
In this representation one or more chemical reactions are specified but they are assumed to be infinitely
fast. In modelling of combustion processes, this approach is known in terms of the “mixed is burned”
assumption. The reactions are completely controlled by the mixture fraction since reactants are
converted directly to final products with a one-step description. So it is enough to solve the balance
equation for the mixture fraction variable and then calculate mass fractions and temperature. This
approach is valid only for low Mach number flow with constant thermodynamic pressure, same
species heat capacities, Lewis number equal to unity and molecular diffusivities all equal to
The equation for the mixture fraction is:
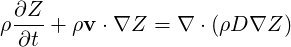 | (4.75) |
Once the solution is known in the entire flow field, the flame surface is defined as the surface of
stoichiometric mixture, which is obtained by setting
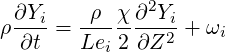 | (4.76) |
where
The complexity added by turbulence comes from the averaging (or filtering) procedure. To determine the average mass fractions and temperature, the mean value of the mixture fraction is not sufficient: higher moments are needed. The two possible approaches are
The eddy dissipation concept, devised by Magnussen and Mjertager (1997), directly extends the Eddy
Break-Up model to non-premixed combustion. The main idea is to replace the chemical time scale of an
assumed one-step reaction by the turbulent time scale 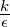 . Thereby the model eliminates the
influence of chemical kinetics, representing the fast chemistry limit only. The fuel mean burning
rate is estimated from fuel (
. Thereby the model eliminates the
influence of chemical kinetics, representing the fast chemistry limit only. The fuel mean burning
rate is estimated from fuel (
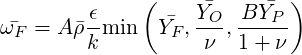 | (4.77) |
where A and B are modelling constants. For a highly exothermic reaction (combustion), 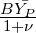 is included
because it is proportional to the heat release and therefore models the temperature dependence of the
reaction. For isothermal reactions this term can be dropped.
is included
because it is proportional to the heat release and therefore models the temperature dependence of the
reaction. For isothermal reactions this term can be dropped.
The eddy dissipation concept is based on the assumption that scalar mixing lengthscales and turbulent
lengthscales are the same, i.e. the concentration is uniform within a Kolmogorov length-scale. This is
only valid for unity Schmidt number (observed in gas phase reactions) but not for Sc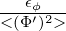 ) one can derive an algebraic equation
depending on the Schmidt number. There also exist more complex models which involve the
solution of transport equations for the variance in different parts of the Kolmogorov energy
spectrum.
) one can derive an algebraic equation
depending on the Schmidt number. There also exist more complex models which involve the
solution of transport equations for the variance in different parts of the Kolmogorov energy
spectrum.
The Boussinesq approximation can be used to solve natural convection problems without
having to solve the full compressible Navier-Stokes equations. This is achieved by selectively
considering local variations in density, due to local variations of temperature, only for the gravity
term in the Navier-Stokes equations. All remaining properties and terms remain unaffected.
The variation of density with temperature is linearized around a set reference density
Variations of density are then approximated through the linear relation
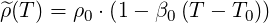 | (5.1) |
For Newtonian fluids, the viscosity is a constant that defines the ratio of stress-to-strain-rate is constant. This property is false for so-called Non-Newtonian fluids. This section describes the capabilities of TransAT for handling such Non-Newtonian fluids.
The Bingham model may be used to describe plastic materials, which feature a yield stress. In this
model, the viscosity
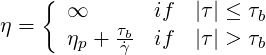 | (6.1) |
where 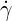 is the shear rate,
is the shear rate,
The Casson model has been developed to simulate plastic materials. In this model, the viscosity is defined by
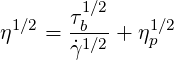 | (6.2) |
where 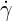 is the shear rate,
is the shear rate,
The power-law model is a simple model for the simulation of pseudo-plastic or dilatant fluids. Viscosity in the power-law model reads
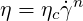 | (6.3) |
where 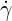 is the shear rate, and
is the shear rate, and
The Carreau model may be used for polymeric liquids. it reads
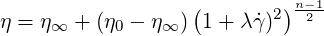 | (6.4) |
where 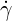 is the shear rate. The zero-shear viscosity
is the shear rate. The zero-shear viscosity
It reads
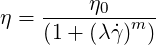 | (6.5) |
where 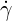 is the shear rate. The zero-shear viscosity
is the shear rate. The zero-shear viscosity
The Carreau-Yasuda model may be used for the simulation of polymers. The viscosity is then written
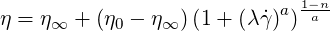 | (6.6) |
where 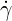 is the shear rate. The zero-shear viscosity
is the shear rate. The zero-shear viscosity
The Thixotropic model may be used for the simulation of crude oil. The viscosity is is a function of a
scalar quantity
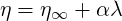 | (6.7) |
where the infinite-shear viscosity
 | (6.8) |
where 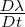 is the substantial derivative of
is the substantial derivative of
The Hershel-Bulkley model may be used to describe In this model, the viscosity
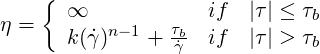 | (6.9) |
where 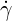 is the shear rate,
is the shear rate, 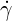 )
)
For Newtonian fluids, the stress is simply the sum of the pressure gradient and the newtonian stress. A more general description is:
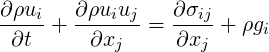 | (7.1) |
where
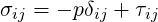 | (7.2) |
where
For a newtonian or viscoplastic fluid (no elastic behaviour), the viscoelastic stress becomes the viscous stress:
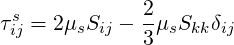 | (7.3) |
For viscoelastic fluids the viscoelastic stress becomes:
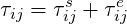 | (7.4) |
where
In general, the response of a viscoelastic material cannot be described with a single characteristic time scale. This is why the more accurate viscoelastic models are the so-called multimode models which can be described as:
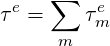 | (7.5) |
where each
The momentum equation then reads:
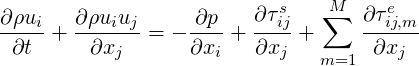 | (7.6) |
The role of the viscoelastic solver in
The stress equation (for one mode) for the Olroyd-B model is:
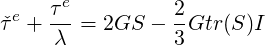 | (7.7) |
The only model parameters that are required (for each individual mode) are the elastic time scale 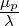 ).
).
The exponential PTT model writes:
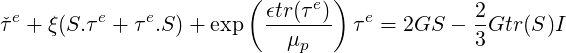 | (7.8) |
The linear PTT is the linearized version of the exponential PTT and writes:
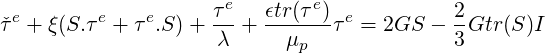 | (7.9) |
For both PTT models the required parameters are (for each mode):
Usually viscosity correction using the Arrhenius law writes:
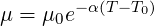 | (7.10) |
where
The viscoelastic solver is currently not available for homogeneous and algebraic slip multiphase models, only with level-set. The properties of each phase are weighted using the level-set function and the procedure is the same than for single phase viscoelastic flows.
The solution of the viscoelastic constitutive equation is made difficult by the high Weissenberg number
problem (HWNP) which occurs when the Weissenberg number reaches moderately high values. The
origin of this numerical is not well explained but seems to correspond to loss of positivity of
conformation tensor
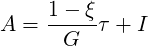
The formulation of the constitutive equation in terms of the matrix logarithm of the conformation tensor has the advantage of not exhibiting such unstable behavior. Transforming the stress equation to obtain the LCT equation results in an equivalent for the stress equation, that needs to be solved and coupled to the momentum equation.
The Rosseland Model (also known as diffusion approximation model) for radiation has been implemented in TransAT. This model can be quickly described as follow:
The Rosseland model assumes that the radiation can be taken into account as a temperature-dependent conductivity. This means that no additional equation is solved, but an effective thermal conductivity is calculated to account for radiative heat transfer.
The radiative heat transfer writes:
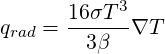
where
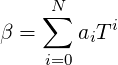
The
This is often a rough approximation because the radiative properties of media are also
spectrum-dependent. This means that the above approximation for
The radiative conductivity can then be calculated as a sum of contributions over the radiation bands.
Immersed boundary (IB) techniques were developed in the late nineties for the simulation
of flow interacting with solid boundary (see for review Mittal & Iaccarino (2005)), under
various formulations. The most widely recognised formulation for instance employs a mixture
of Eulerian and Lagrangian variables, where the solid boundary is represented by discrete
Lagrangian markers embedding in and exerting forces to the Eulerian fluid domain. The
interactions between the Lagrangian markers and the fluid variables are linked by a simple
discretised delta function. The IB methods are all based on the direct momentum forcing
(penalty approach) on the Eulerian grids, with various forcing formulations on the Lagrangian
marker. The forcing should be performed because it ensures the satisfaction of the no-slip
boundary condition on the immersed boundary in the intermediate time step. This forcing
procedure involves solving a banded linear system of equations whose unknowns consist of the
boundary forces on the Lagrangian markers, thus, the order of the unknowns is one-dimensional
lower than the fluid variables. Numerical experiments show that the stability limit can in
general be altered by the proposed force formulation, in that the second-order accuracy
of the adopted numerical scheme is degraded to first order, and in the best conditions to
1.5.
The Immersed Surfaces Technique (IST) has been developed as part of TransAT, although other
similar approaches have been developed in parallel. It is implemented in the CMFD code TransAT. The
underpinning idea is inspired from the Level Set interface tracking technique for two-phase flows, where
free surfaces are described by a hyperbolic convection equation. In the IST, the solid is
described as the second phase, with its own thermo-mechanical properties. The technique differs
substantially from the IB method discussed above, in that the jump condition at the solid surface is
implicitly accounted for, not via direct momentum forcing (using the penalty approach)
on the Eulerian grids. It has the major advantage of being able to solve conjugate heat
transfer problems, in that conduction inside the body is directly linked to external fluid
convection.
A simple example is reported in Figure 9.1, consisting of the flow past a conical shape or a
round-shaped structure. The solid is first immersed into a cubical grid covered by a Cartesian mesh. The
solid is defined by its external boundaries, which will be described by a sort of level set function denoted
by

The immersed surface is represented on the fluid grid by a Level Set function (
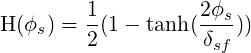 | (9.1) |
where,
We present the fluid conservation equations for the case where the solid is stationary and the solid
velocity is set to zero (
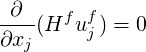 | (9.2) |
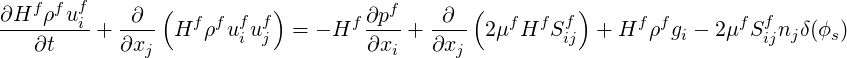 | (9.3) |
the last term in the RHS is a viscous shear at the wall, where
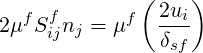 | (9.4) |
When used in combination with RANS turbulence modelling and wall–functions, the wall shear is calculated using the logarithmic law of the wall.
For an immersed surface TransAT can solve for the temperature distribution inside the solid. This
separate equation for solid temperature is termed TSolid for short in the user manual and the graphical
user interface.
For TSolid the steady state heat conduction equations are solved inside all solids selected
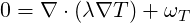 | (9.5) |
where
Boundary conditions can be of the Dirichlet (constant temperature) or the Neumann (constant heat
flux) type. Spatial variation in the boundary condition value is allowed.
Evolutionary Genetic Algorithms (EGAs) are a family of computational models inspired by Darwin’s
evolution theory. These algorithms liken potential solutions to specific problems chromosome-like
structures. Recombination operators are applied to these structures such that critical information is
preserved. Despite being often viewed as function optimizers, genetic algorithms are applied to solve a
wide range of problems.
A genetic algorithm implementation begins with a population of chromosomes (i.e. sets of parameters)
which is expanded from generation to generation. The fitness of each chromosome is evaluated at each
generation. The fitness of chromosomes is the determining factor for the generation of the
following generations. Chromosomes of the next generation are produced by a reproduction
operator.
From one generation to the other, the reproduction operator produces new chromosomes by means of
mutation and crossover. The reproduction operator is implemented in such a way that it biased towards
the fittest solutions of the population.
As the EGA progresses, the fittest solutions should prevail. The EGA is stopped if the convergence
criteria of the EGA or the maximum number of generation are reached. The EGA can also be stopped
earlier if the solution obtained from a chromosome meets the targets set for a satisfactory solution. In
the case of the EGA implemented in
The EGA of the SArP module is a controller built around the numerical solver of
The only information required to make the EGA progress over generations is the knowledge of the
fitness of the individuals to sort them. The fitness of the individuals is obtained by evaluating the
so-called fitness function. The fitness function is based on objectives (e.g. target residuals, physical time
constraint, etc.).
The problem statement can be expressed in terms of fitness function as follows:
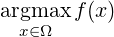 | (10.1) |
where Ω is the set of chromosomes (i.e. the set of numerical parameters) and
The flowcharts in Figure 10.2 and Figure 10.3 show the different stages. Figure 10.2 gives a
general overview of the process while Figure 10.3 goes into more details about the selection
process.
As shown in Figure 10.3, the initial population of the EGA is generated by altering the original set of
parameters i.e. chromosome. New chromosomes are produced at every generation by means of mutating
the fittest individual with the aim of enhancing the fitness. In a nutshell, a population made
of N individuals, comprises one original chromosome and N-1 mutations of that original
chromosome. The mutation rate, probability to carry out a mutation on a chromosome, is set at a
high value to guarantee a variety of chromosomes in the population. With high mutation
rates, the search space is wider and it reduces the risk of encountering a local optimisation
problem.
Chromosomes are composed of genes. The genes are the individual parameters used to set numerical solvers. These parameters can be of one of the three types:
The ranges of the different genes were set accordingly to the options available in
To avoid unnecessarily increasing the computation time, the EGA should only be used when a
simulation diverges, crashes or does not converge fast enough. The activation conditions and
the steps performed by the EGA vary depending on the type of simulations, stationary or
transient.
The EGA has two modes which are depicted in the flowcharts of Figure
In stability mode, the EGA is launched upon occurrence of one of the following conditions depending on the type of simulation:
The convergence of the residuals is estimated by computing the slope of the linear function fitting the point cloud of residuals for each equation. The linear function is computed using the least squares method.
Similarly to residual convergence in steady cases, the time-step duration decrease is measured by fitting a linear function to the point cloud of time-step duration.
The EGA stops when one of the stopping criteria is met. The stopping criteria vary accordingly to the nature of the simulation, steady or unsteady. For steady cases, the EGA stops if:
A typical steady simulation fitness evaluation is shown in Figure 10.6. In that example the residuals exit
condition is met by the variable represented with red disks and green crosses since their residuals drop
below
For unsteady cases, the EGA stops if:
Genetic operations are used to create new chromosomes based on an existing population. The genetic operations consist in applying chromosome crossover followed by mutation in each generation except the first one where the mutation operation is applied directly on the original set of parameters.
Mutation is only applied on a random number of new chromosomes. Mutation is then applied on a
random set of genes, which size (ratio of number of genes in set to total number of genes in
chromosome) is equal to the mutation rate. Thanks to mutation, the parameters space is more
thoroughly explored which in turn prevents the algorithm from getting stuck in an area around a local
minimum.
There is a mutation operator for each type of parameter. They operate as follows:
The implemented crossover operation is based on a one-point crossover. According to the encoding
method and the predefined physical rules, the overall consistency of the underlying solution and the
validity of the individuals in the population must be maintained. To make sure that genes and
combination of genes are within the possible ranges, an extra correction step is added in the breeding
process of the EGA. These corrections allow avoiding crashes or unphysical solutions in
The basic part of the selection process is to stochastically select from one generation to create the basis of the next generation. The requirement is that the selection process should make the chances of survival of the fittest individuals greater than weaker ones. This replicates natural selection process in that fitter individuals will tend to have a better probability of survival and will go forward to form the mating pool for the next generation. Weaker individuals are not without a chance. In nature such individuals may have genetic coding that may prove to be useful for future generations.
In each generation, chromosomes are accordingly evaluated with
The fitness function indicates the fitness of a chromosome and serves as a metaheuristic to initiate the
genetic algorithm. The multi-objective fitness function used to deduce the fitness of chromosomes is
defined as a linear combination of simulation runtime efficiency and convergence quality. The
distance to the target, quality of convergence and stability are the input variables to the fitness
function.
Different indicators determining how good a simulation converges are isolated and weighted in the
fitness function. In order to take the different weights of the indicators into account, the indicators are
multiplied by weighted coefficients in the fitness function definition.
The stability and the quality of convergence at a point
The fitness function reads:
![∀i ∈ [w, N ] fi(di,ci,ei) = - αi|log(di)|- βici - γ|log(ei)|](TransAT_algorithms_handbook258x.png) | (10.2) |
Where:
For stationary simulations, the fitness function is exactly as defined in Eq. 10.2. For transient
simulations, two extra terms are appended to the fitness function definition in Eq. 10.2. One
is related to the convergence of the last time step and the other to the duration of time
steps.
For steady cases, the following sequence of filtering is performed to select the fittest chromosome:
For unsteady test cases, the selection process is different than with steady test cases. The selection is done sequentially:
To extract the fittest individuals, different selection strategies from the DEAP module (Fortin
The
In theory, the fitness of a chromosome is obtained by evaluating the fitness function which means
running a simulation. Bearing in mind the number of simulations required to run to evaluate the fitness
function (one for each chromosome produced during the EGA process), running the EGA can be
computationally costly.
To offset the potential excessive cost of the EGA, estimation models predicting the fitness based on past
fitness evaluations implemented in the SArP module can be used. Instead of letting the EGA progress
naturally – i.e. by evaluating the fitness with a
The aim is to select more fitting individuals to be eventually evaluated with
The proposed solution in the SArP module is based on machine learning techniques such as non-linear
regression models and decision trees.
The idea, as detailed in the previous diagram, is to launch the EGA in order to feed the machine
learning algorithm with its output data. Indeed, the data used to feed the machine learning algorithms
comes from a local database that is expanded by runs of the SArP module with fitness prediction
enabled. When fitness prediction is enabled, fitness evaluations of chromosomes evaluated during the
EGA are added to that local database.
If the database is large enough, it can be used to refine the machine-learning models. When prediction is
enabled, the fitness of the chromosomes of a generation is first estimated using the prediction algorithms
of machine-learning models. A set of half the population size consisting of the fittest elements is then
extracted from the population to be evaluated using
As shown in Figure 10.8, the SArP module executes the following steps when prediction is enabled:
Two types of machine-learning models were implemented: classifiers and regressors.
The former type of model has a binary behaviour. Chromosomes can be either fit or unfit depending on
their fitness. These chromosome classes are uniformly distributed within the data from the database.
This classification method is an efficient way to eliminate cases that are quickly diverging.
Although this model cannot order two solutions in the same class, it remains faster than
regressors.
With regressors, regression is used to predict the actual value of the fitness value. It gives more accurate
results than with classifiers. The estimation of the fitness function as a continuous function allows the
differentiation and ordering of chromosomes. Non-linear regression models are used to handle the
complexity of the problems at hand.
The list of implemented algorithms, based on the scikit-learn API (Buitinck
The main strategy to speed up the EGA is to reduce the number of evaluations performed during the correction and optimisation process. There are three main options to do this:
Note that all three options can be coupled as thy are independent from one another.
Alternatively, the EGA can be stopped in the middle of the process if a satisfactory solution
has been found. This can be done by clicking ![]() in the
in the